从评分到对决：借鉴ELO思想重塑AI搜索排序

在构建如 RAG 或 AI 代理这类人工智能系统时，检索的质量是决定系统上限的关键。开发者通常依赖两种主流检索技术：关键词搜索和语义搜索。

• 关键词搜索 (例如 BM25): 速度快，擅长精确匹配。但一旦用户提问的措辞改变，召回率就会下降。
• 语义搜索: 通过向量嵌入捕捉文本的深层含义，能理解概念性的查询。

一个常见的实践是结合两者来最大化召回率。然而，高召回率不等于高精确率。即便正确答案被包含在海量的召回文档中，如果它排在第67位，大语言模型或用户基本不可能看到它。为了解决“顶针沉海”的问题，reranker (重排序器) 应运而生。

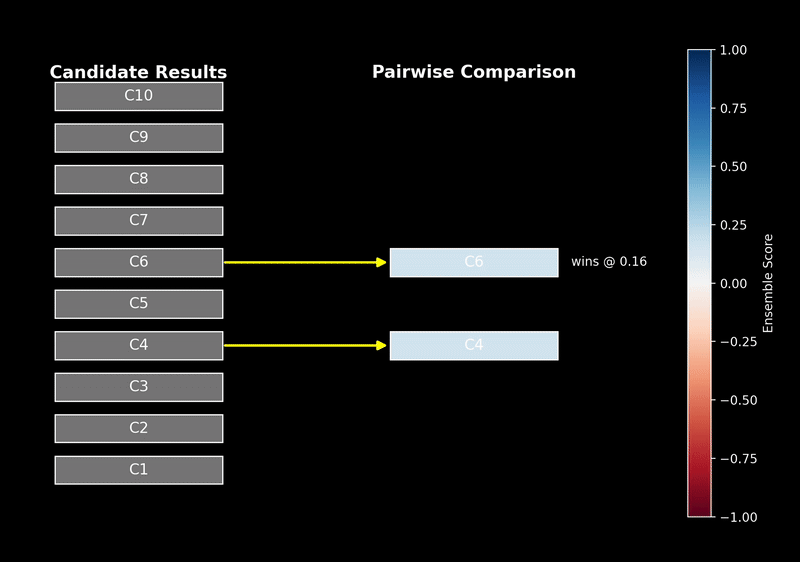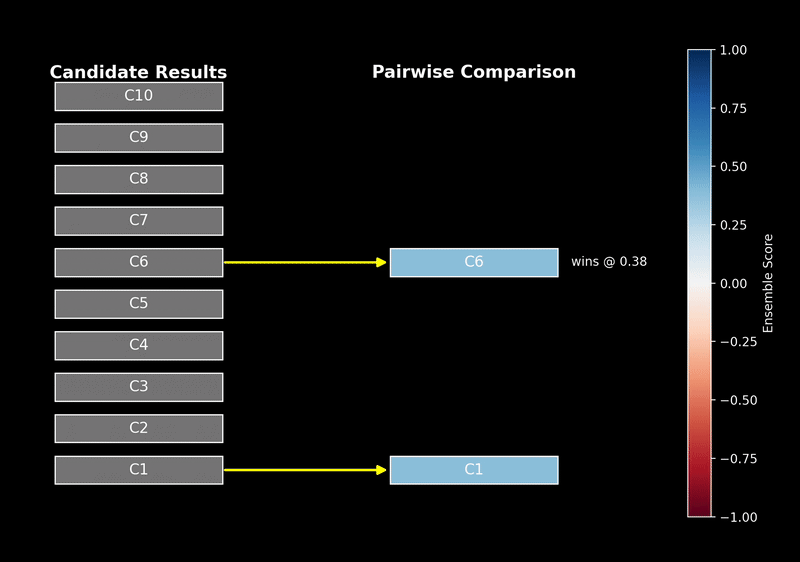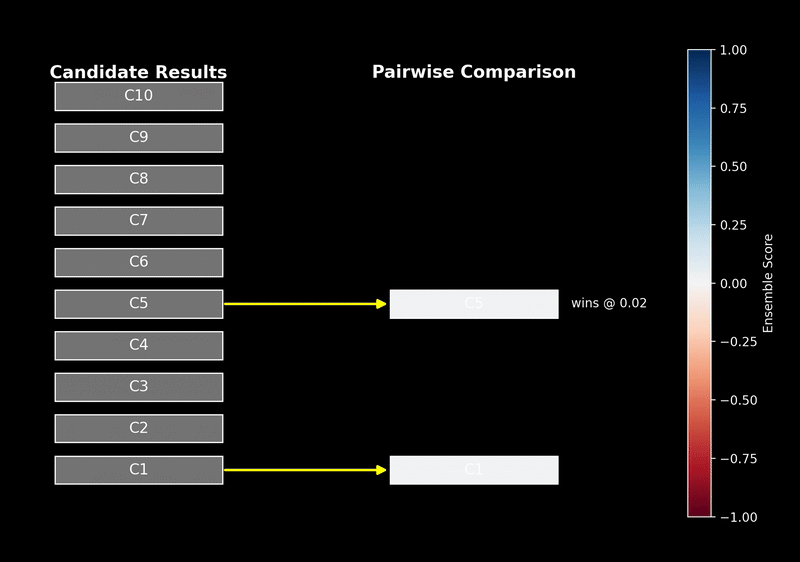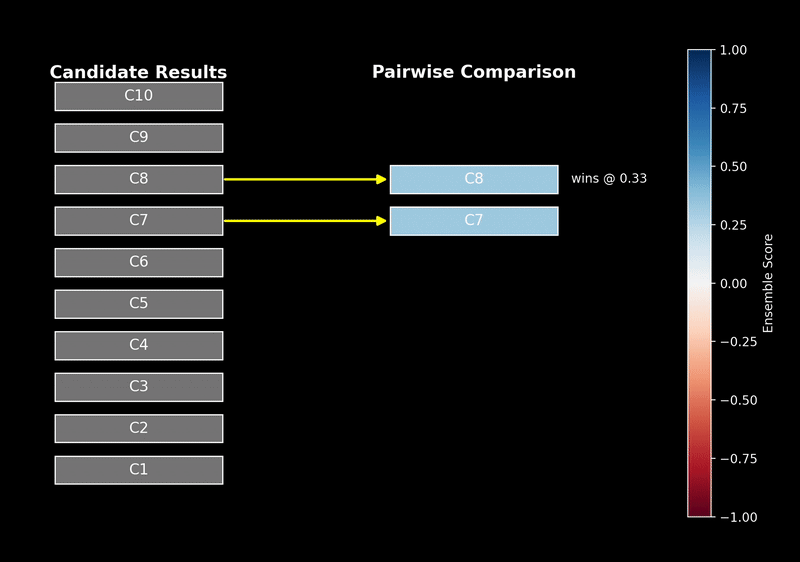
什么是Reranker？

可以把 reranker 理解为信息检索流程中的“复赛评审”。

初级的关键词或语义搜索如同“海选”，快速从海量文档中筛选出几百个相关的候选者。但海选过程相对粗糙，文档是独立于查询被编码的。而 reranker 作为复赛评审，会拿到用户的“查询”和每个“候选文档”的全文，进行精细化的比对和打分，最终给出一个更权威、更符合用户真实意图的排序。因为它同时接触查询和文档，所以对上下文的理解远超海选阶段。

本文将介绍一种全新的 reranker 训练方法，它摒弃了传统的评分标注，转而借鉴了在国际象棋和电子竞技中广泛使用的 ELO 等级分系统。

问题的核心：评分的不可靠性

训练 reranker 的目标是创建一个函数 f(q, d)，它能为任何“查询 q”和“文档 d”生成一个精准的相关性分数 s。理论上，只要有海量的 (q, d, s) 数据，就可以通过监督学习训练出一个神经网络。

但问题在于，这个“分数 s”极难获得。

现有方案的困境：二元标注与“假阴性”灾难

当前的主流方法是使用人工标注的“正例”（相关）和“负例”（不相关）数据对。正例好找，但负例的构建却是个大问题。

一种方法是从全部文档中随机抽取，认为它大概率不相关。但这就像让一个拳王去打一个普通人，训练出的模型无法处理那些“看起来有点关系，但实际没用”的微妙情况。

另一种方法是使用 BM25 或向量搜索的结果作为负例的来源。但这引发了“假阴性”灾难：你怎么知道一个被标记为“负例”的文档，它真的不相关？答案是，你不知道。在很多情况下，一个被当作负例的文档，实际上比所谓的“正例”更相关。

这种评分体系的模糊性是根本问题。人类大脑本身就不擅长给事物打绝对分数。

查询: “谁赢得了2017年诺贝尔物理学奖？”
文档: “引力波于2015年由LIGO首次观测到。”

这个文档应该打多少分？有人可能觉得年份不对，打低分；但物理爱好者知道，2017年的诺奖正是授予给了引力波的发现者，因此会打高分。这种巨大的主观差异使得绝对评分充满噪声。

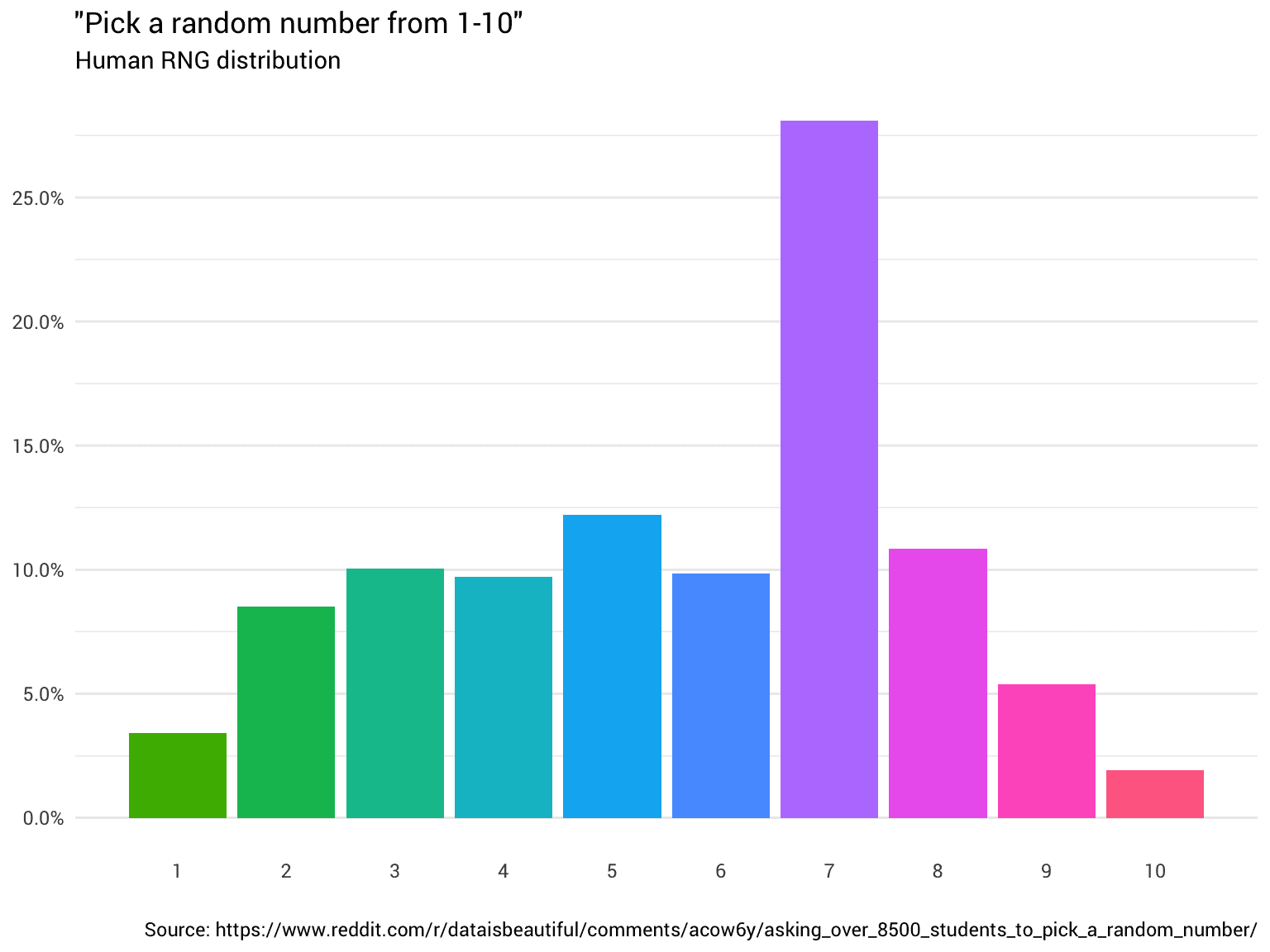
解决方案：从“评分”转向“比较”

如果绝对评分不可靠，那我们能否只进行比较？人类大脑虽然不擅长绝对评估，但极其擅长相对判断。

查询: “谁赢得了2017年诺贝尔物理学奖？”
文档1: 诺贝尔奖颁发给了那些在2015年发现引力波的人。
文档2: 引力波于2015年9月由LIGO引力波探测器首次观测到。

几乎所有人都会认为，文档1比文档2更相关。通过成对比较，我们获得了信噪比极高的标注数据。这正是 ELO 评级系统的核心思想：不问“你有多强”，只问“你和另一个人谁更强”。通过大量的两两对决结果，我们可以为每个“选手”（文档）计算出一个相对精确的排位。

现在，问题转化为如何将大量的成对比较结果，转换成一个可用的绝对分数向量。

训练流程概述

基于此，一个创新的训练管线被设计出来：

1. 三元组采样与标注: 对每个查询，初步检索100个候选文档。随机抽取文档三元组 (q, d_i, d_j)，让大语言模型（LLM）集群判断 d_i 和 d_j 哪个更相关。
2. 训练成对比较模型: 使用 LLM 的标注数据，训练一个轻量级的成对 reranker，使其能高效地预测任意两个文档的相对优劣。
3. 计算ELO分数: 对每个查询的候选文档，利用上一步训练好的模型进行多轮“模拟比赛”，然后使用 ELO 算法为每个文档计算出等级分。
4. 训练最终模型: 将 ELO 分数作为“标准答案”，训练一个标准的、单点式的 reranker，使其能够直接预测文档的相关性分数。
5. 强化学习微调: 在监督学习之后，引入强化学习，让模型通过自我试错进一步优化排序策略，提升最终性能。

核心技术：成对比较与ELO评级

训练成对比较器

首先，研究团队使用3个 LLM 组成的集成模型，对大量的文档对 (d_i, d_j) 进行优劣判断，生成一个 [0, 1] 之间的偏好分数。这个过程成本很高，因此其目标不是直接应用，而是生成高质量的训练数据。

随后，这些数据被用来微调一个轻量级的开源模型，训练出一个高效的“成对比较器”。

获取ELO评级

ELO 模型预测选手 i 战胜选手 j 的概率基于他们的等级分之差 e_i - e_j。预测公式为：

p_ij = p_i / (p_i + p_j)

其中，p_i = 10^(e_i / 400)。通过这个公式，我们可以将概率与等级分关联起来。

有了大量的成对比赛结果（由上一步的比较器生成），就可以通过最大似然估计来拟合出最能解释这些比赛结果的 ELO 分数 e_i, e_j, ...。损失函数如下：

𝓁 = -∑_{i, j}w_ijlog(p_i/(p_i+p_j)) = ∑_{i, j}w_ijlog(1+e^e_j-e_i)

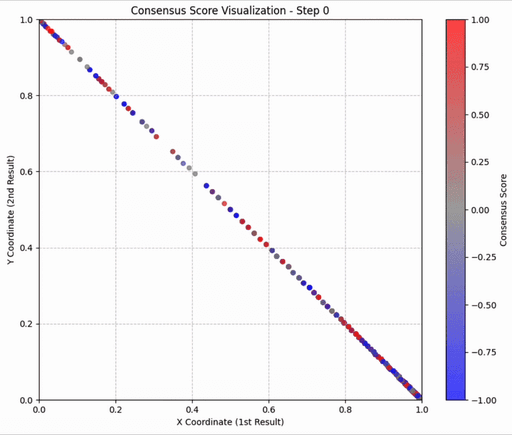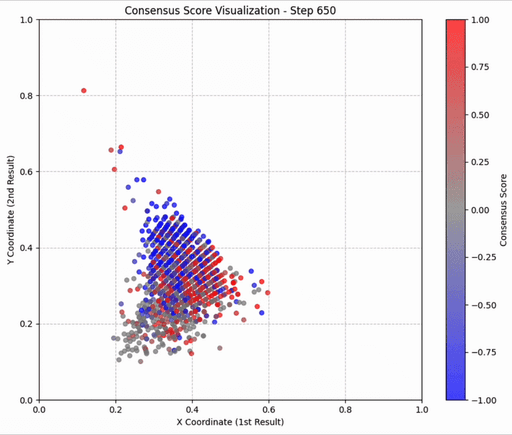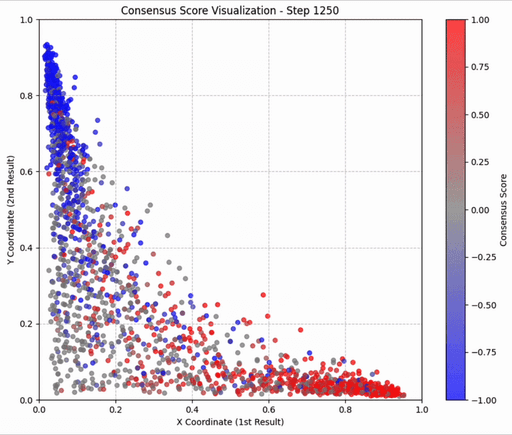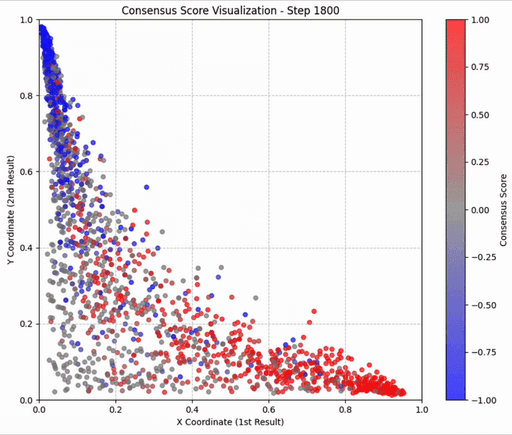
在实践中，对每个查询的100个文档进行全部 n² 次比较是不现实的。研究发现，仅采样 O(n) 次比较（例如，构建几个随机的比赛环路）就足以获得与完全比较几乎一致的 ELO 分数。

跨查询偏差调整

上述 ELO 计算是在单个查询的内部完成的，这会带来一个新问题：

1. 对于一个没有好答案的查询，最不差的那个文档也会获得很高的相对 ELO 分（差生里的第一名）。
2. 对于一个有很多好答案的查询，一些相当不错的文档可能会获得很低的相对 ELO 分（优等生里的末尾）。

这会严重误导最终模型的训练。为了解决这个问题，需要引入一个“跨查询偏差 b”来校准不同查询之间的分数基准。

其核心思路是，让模型不仅能比较“同一个问题下的两个答案”，还要能比较“两个不同问题下的各自答案”，即 (q_1, d_1) 与 (q_2, d_2) 哪个相关性更高。这种“苹果对橘子”的比较虽然噪声更大，但它为我们提供了校准不同查询难度所需的关键信息。通过一个更复杂的 ELO 模型，可以为每个查询计算出理想的偏差 b，公式大致如下：

P(P₁ > P₂) = (p₁ + b₁) / ((p₁ + b₁) + (p₂ + b₂))

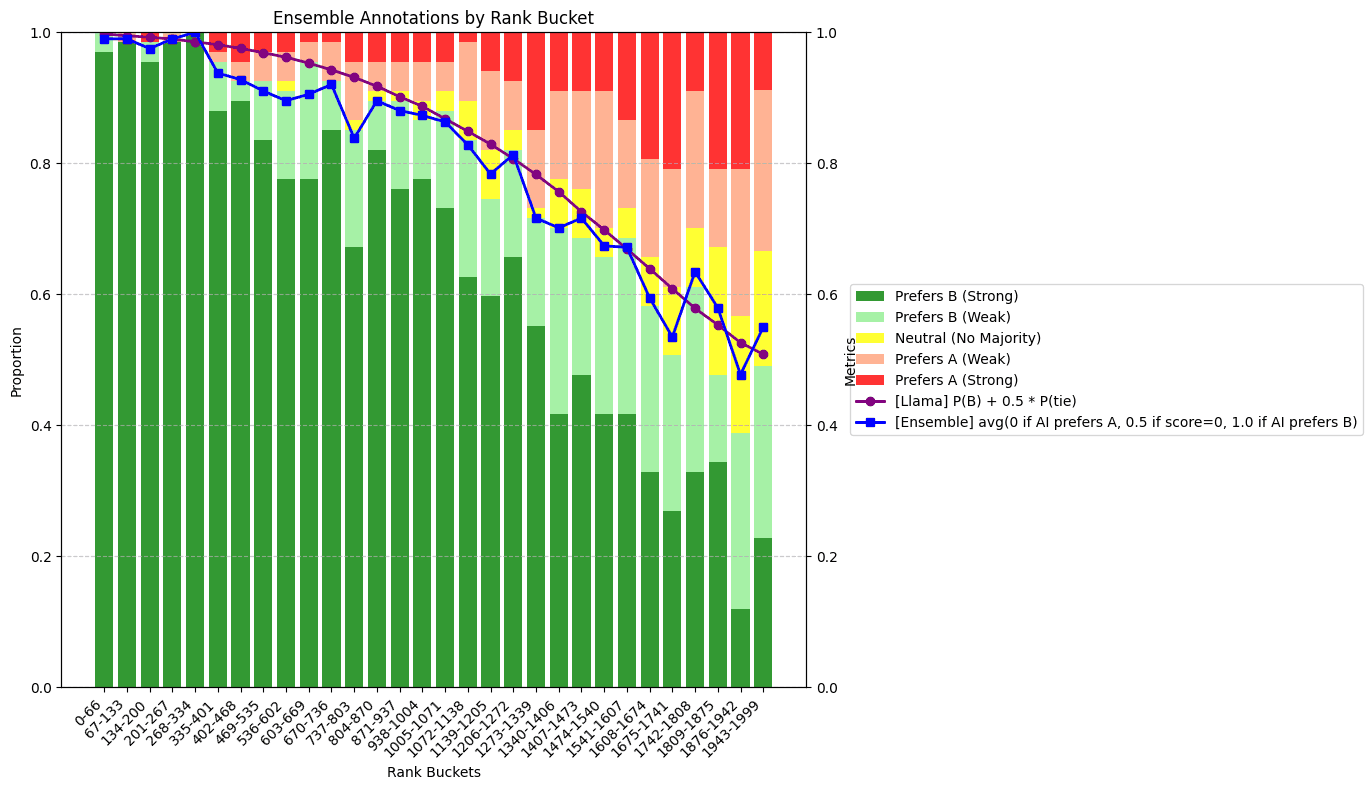
训练单点式模型

通过以上步骤，一个能够生成高质量、有意义的绝对分数 f(q, d) = elo(q, d) + b(q) 的函数被创造出来。

最后一步，就是用这个函数产生的数据集，通过标准的均方误差损失，来监督微调一个最终的 reranker 模型。研究团队发现，在 Qwen 模型家族上进行微调能产生最佳效果，这便催生了 zerank-1 和 zerank-1-small 模型。

这种以数学建模为核心，通过 ELO 系统生成高质量训练数据的方法，代表了 reranker 领域的一个独特且有效的探索方向。它从根本上解决了传统方法中因依赖不可靠的人工绝对评分而导致的噪声和瓶颈问题。