プロンプティングの新しいアプローチ - アナロジカル・プロンプティング

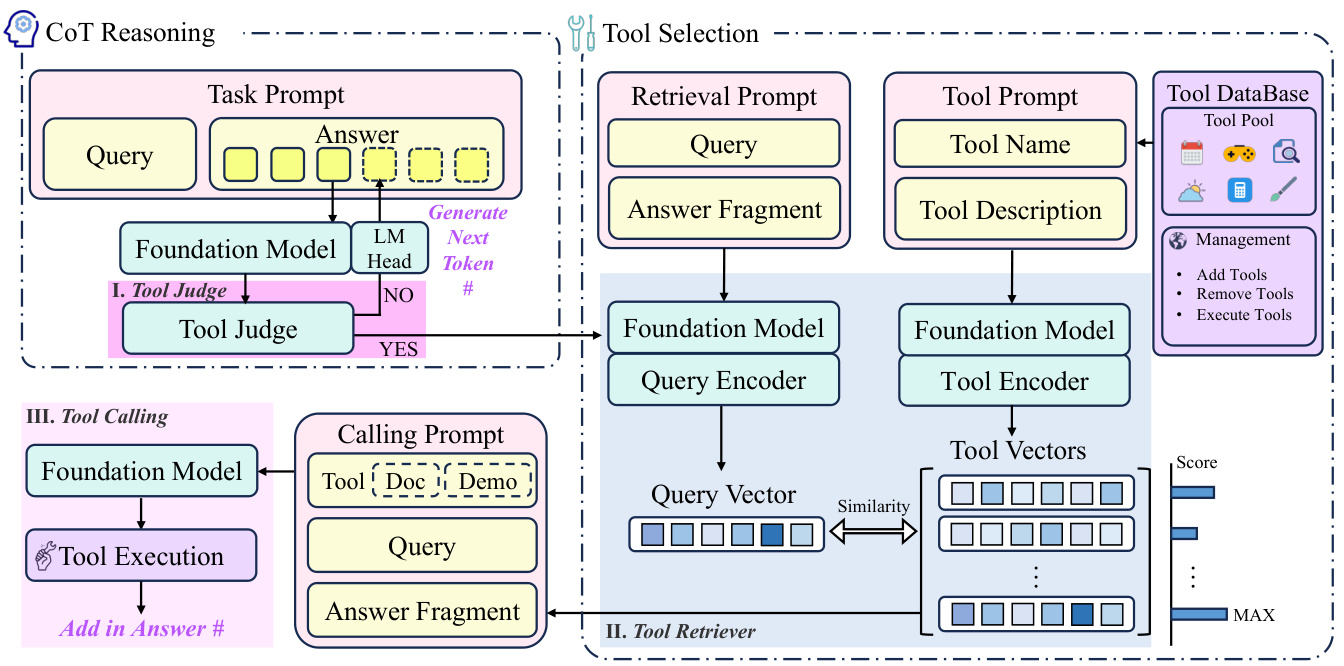
という興味深い論文を読んだ。類推モデルとしての大規模言語モデル アナロジカル・プロンプト（類推的プロンプト）」というプロンプトへの新しいアプローチがある。

LLMの推論能力を大幅に向上させるCoT(Chain of Thought)は、キューエンジニアリングに詳しい方なら一度は耳にしたことがあるはずだ。しかし、CoTを使用する場合、モデルを導くための適切なガイダンスや推論例を提供する必要があります。

0ショットCoTとは、プロンプトの中で推論のステップを明示的に与え、LLMに推論を完了するためのステップを参照させることである。0ショットCoTはプロンプトの中で推論のステップを明示的に与え、LLMにそのステップを参照させて推論を完了させる。

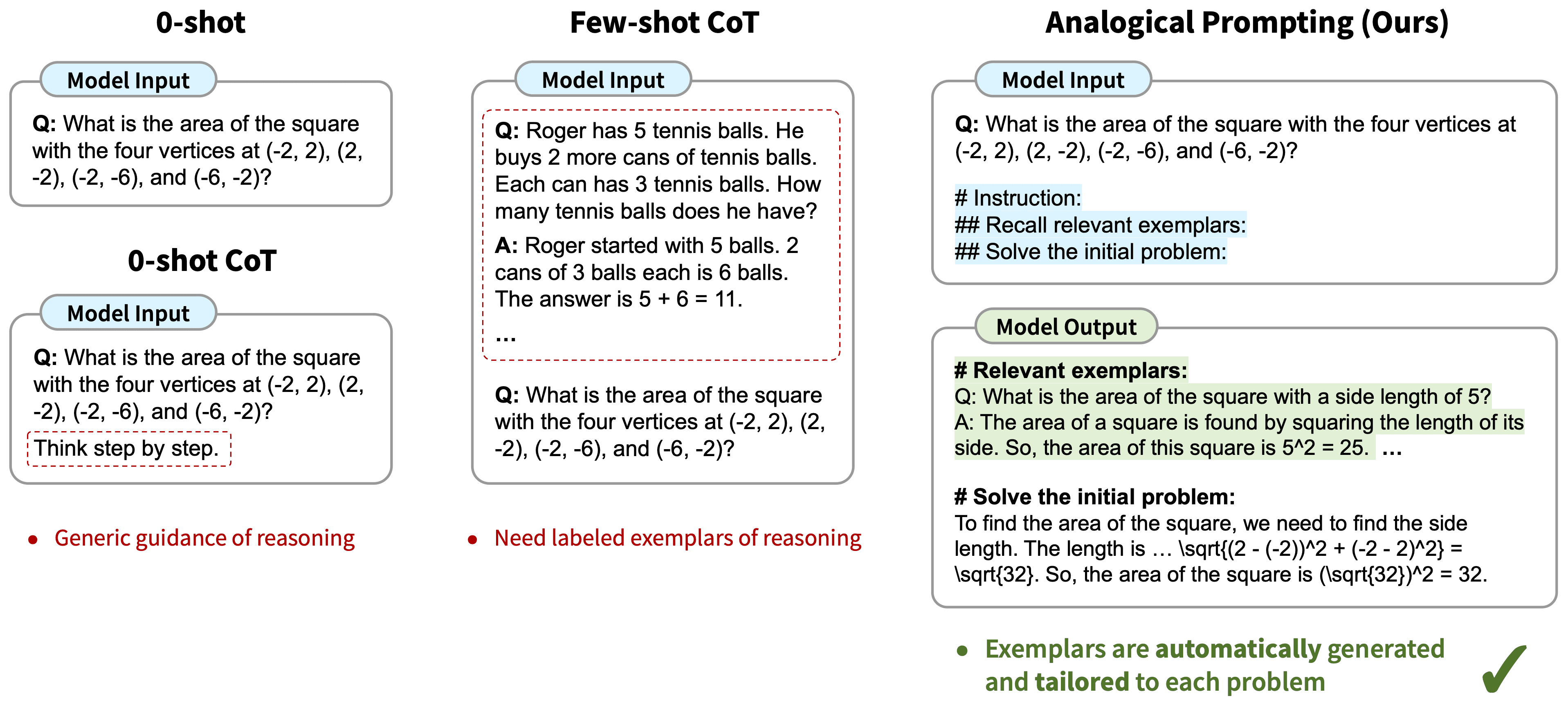
3つのプロンプティング方法の比較

例えば、「4つの頂点が（-2、2）、（2、-2）、（-2、-6）、（-6、-2）である正方形がありますが、この正方形の面積はいくらですか？"

もしCoTを使わないのであれば、LLMに問題を投げかけて答えを出させることになる。この問題はGPT-4では解けるはずですが、GPT-3.5では間違っている可能性が高く、推論が弱い他のモデルではなおさらです。

もし0ショットCoTを使うのであれば、例えばプロンプトの中で推論ステップを明示的に与えればいい：

以下の手順で計算してください：
1, まず、隣接する2つの頂点間の距離を正方形の辺の長さとして計算する。
2、辺の長さの2乗を計算し、正方形の面積を求める。

これらのステップに従えば、GPTが3.5のLLMで正しい結果が得られるはずだ。

もし数発のCoTを使うのであれば、それは例えば少数の例を示していることになる：

Q: 4つの頂点が(0, 0)、(1, 1)、(0, 1)、(1, 0)の正方形がある。
A: 隣接する2つの頂点、例えば(0, 0)と(1, 1)を選び、それらの距離を計算して辺の長さを1にし、辺の長さの2乗を計算して面積を1にする。
Q: (-2, 2), (2, -2), (-2, -6), (-6, -2)を4頂点とする正方形がある。

GPT-3.5を搭載したLLMが正しい結果を得られるように、プロンプトで明示的に例を示し、LLMに例のステップに従うように指示します。

では、「類推的キューイング」とは何か？

学校で数学を習ったときのことを考えてみよう。このような数学の問題を解いたら、似たような問題をやったことがあるかどうかを考えるだろう。特に私のような小さな町の問題児にとっては、当時何枚のペーパーを解いたかわからない。だから、部屋の後ろで問題を見たときに、前に似たような問題をやったことがあることを思い出せば、すぐに答えを思いつくことができる。

LLMの知識の蓄えは人間のそれよりも強く、トレーニングの間にあらゆる知識や事例を蓄積している。

つまり、「類推ヒント法」とは、LLMにまず問題を解かせようと焦らせるのではなく、まず問題に関連する例をいくつも挙げさせ、それらの例を使って問題を解くための推論をさせることである。これは、LLMに数撃ちゃ当たるを書かせ、思考の連鎖を生み出す手助けをさせることに等しい。

数学の問題を手に入れたとき、まずその数学の問題をたどって似たような例題や参考解答を見つけ、その例題や参考解答をたどって元の問題を解くように求めるのと似ている。

プロンプトの構成は以下の通り：

最初の質問： 〚<元の質問
関連する問題：関連するユニークな問題を3つ思い浮かべ、それぞれの問題とその解決策を説明する。
最初の問題を解く：

LLMに、問題を受け取ったら、関連する3つのユニークな問題を想起させ、それぞれの問題と解決策（できればステップ付き）をリストアップさせ、必ず中間過程をプリントアウトさせる。LLMがこれらの関連する例を出力し終えたら、元の問題を（忘れないように）もう一度プリントアウトし、LLMがこれらの関連する例を使って元の問題を推論できるようにする。

アナログ・ヒンティングを使ったプロンプトの完全リファレンス：

あなたの課題は数学の問題を解くことです。数学の問題が提示されたら、例題として関連するトピックをいくつか思い出してください。そして、一番最初の問題に戻って解きましょう。

# 一番最初の質問：

ある航空会社では、機内でステーキか魚を選べるディナーを乗客全員に提供している。6人の乗務員のうち3人はステーキを、3人は魚を選ぶことができる。料理が無作為に割り振られる場合，パイロットが2人とも魚を選ぶ確率は何％か．

#操作ガイド：

答案には以下の点を含めること：

##関連問題：

例題として、一番最初の問題に関連する数学の問題を3つ考えてください。各問題は、最初の問題も含めて、他の問題とは異なっていなければならないことに注意すること（例えば、異なる数や名前を含む）。各問題は以下の形式に従ってください：

– “Q：” 后面写问题描述

– “A：” 后面写问题的解决方法，并把最终答案写在 \boxed 里。

##最初に問題を解決する：

次の数学の問題を解きましょう」と言ってください。 そして、次の形式で答えなさい：

Q：一番最初の質問をコピーしてここに貼り付けてください。

A：解答を説明し、最終的な答えを☑で書きなさい。

LLMは次のように出力する：

##関連問題：

### 質問1：

– **Q：** 在一个派对上，每个人都可以选择吃苹果派或香草冰淇淋。其中，五名女士可以选择吃苹果派，五名女士可以选择吃香草冰淇淋。如果甜点是随机分配的，那么两名女士都拿到香草冰淇淋的概率是多少？

– **A：** 使用组合计算来求解此问题。总的方式是从五名可以选择冰淇淋的女士中选择两名，这有 \( \binom{5}{2} = 10 \) 种方式。而总的分配方式是从十名女士中选择两名，即 \( \binom{10}{2} = 45 \) 种方式。所以概率是 \( \frac{10}{45} = \frac{2}{9} \)。最终答案是 \( \boxed{\frac{2}{9}} \)。

### 質問2：

– **Q：** 在一次晚宴上，每个人可以选择红酒或白酒。有四名男士可以选择红酒，四名男士可以选择白酒。如果酒是随机分配的，那么三名男士都拿到白酒的概率是多少？

– **A：** 采用类似的方法，从四名可以选择白酒的男士中选出三名，有 \( \binom{4}{3} = 4 \) 种方式。而总的分配方式是从八名男士中选择三名，即 \( \binom{8}{3} = 56 \) 种方式。所以概率是 \( \frac{4}{56} = \frac{1}{14} \)。最终答案是 \( \boxed{\frac{1}{14}} \)。

### 質問3：

– **Q：** 在咖啡馆，每个人可以选择拿铁或卡布奇诺。有三名顾客可以选择拿铁，三名顾客可以选择卡布奇诺。如果咖啡是随机分配的，那么一名顾客拿到卡布奇诺的概率是多少？

– **A：** 在这种情况下，我们选择一名可以喝卡布奇诺的顾客，有 \( \binom{3}{1} = 3 \) 种方式。总的分配方式是从六名顾客中选择一名，即 \( \binom{6}{1} = 6 \) 种方式。所以概率是 \( \frac{3}{6} = \frac{1}{2} \)。最终答案是 \( \boxed{\frac{1}{2}} \)。

## 次の数学の問題を解いてみよう。

###問：ある航空会社が飛行機の乗客全員に夕食を提供している。6人の乗務員のうち3人はステーキを、3人は魚を選ぶことができる。料理がランダムに割り振られる場合、パイロットの2人が魚を選ぶ確率は？

### A: この問題にも同様の解法が使える。魚を選べるパイロットが3人いて、そのうちの2人を選びたい。これは、Ⓐの方法で行います。合計すると6人のパイロットから2人を選ぶことになり、その確率はⒶ（Ⓐbinom{6}{2} = 15Ⓐ）通りです。ということは、確率は(￢frac{3}{15} = ￢frac{1}{5} ￢)となります。最終的な答えは Ⓐ です。